Namáhání konstrukcí šachtových přelivů vyvozené axiálním a spirálním proudění

Jednoznačné stanovení namáhání konstrukcí při různých zatěžovacích stavech je nutnou podmínkou spolehlivého návrhu a posouzení nejen vodohospodářských staveb. Zatížení konstrukcí představuje základní vstup do analýzy bez ohledu na následně použitou metodiku posuzování. Stanovení kóty mezní bezpečné hladiny, která je často využívána k prokázání bezpečnosti vodního díla za povodní, se nutně opírá o detailní statickou (a ve vybraných případech) i dynamickou analýzu konstrukcí stejně, jako moderní přístupy rizikové analýzy. V tomto kontextu představuje omezená znalost namáhání tlakovými pulzacemi šachtových přelivů značnou nejistotu se značným potenciálem k rozvoji poruch. Zejména u vysokých šachtových přelivů věžového typu, jejichž funkci či stabilitu nelze v průběhu povodňových situací jakkoli pozitivně ovlivňovat, jsou omezení závažná. Článek shrnuje výsledky studia namáhání šachtového přelivu tlakovými pulzacemi na fyzikálním modelu VD Jirkov při úpravách vtokových podmínek.

1. Úvod

Výstavba sypaných zemních a kamenitých hrází vybavených šachtovými přelivy věžového typu ve druhé polovině dvacátého století vyvolala potřebu stanovení namáhání konstrukcí svislých šachet a přechodových prvků způsobeného tlakovými pulzacemi proudící vody. Hydrotechnické výzkumy navrhovaných vodních děl se ovšem zaměřily v podstatě na bezpečné převedení návrhové nebo kontrolní povodně, a přesah měření do obecného popisu probíhajících jevů byl veskrze omezený. Hydraulické poměry v šachtových přelivech s přechodovými prvky a navazujícími odpadními chodbami jsou velmi komplexní. Nátokové podmínky ovlivňuje nejen přítomnost usměrňujících prvků, bez ohledu zda jejich účelem je zajistit spirální proudění v šachtě nebo jeho vzniku zabránit, ale i samotná poloha přelivu v nádrži a tvar nádrže a samozřejmě samotný tvar přelivné plochy. Ovlivnění způsobené konstrukčními parametry nátoku není při změně hladiny v nádrži konstantní. Tvar přechodových prvků významně ovlivňuje změnu režimu, zahlcení a jeho propagaci do šachty nebo odpadní chodby. Přestože se článek věnuje především šachtovým přelivům s šachtou i nátokem kruhového profilu, obecné závěry pro spirální proudění a tlakové pulzace lze aplikovat i na jiné průřezy.

Tvar přechodového prvku mezi svislou šachtou a odpadní chodbou z pohledu místní hydraulické ztráty při plně tlakovém proudění byl zkoumán na modelech již Gardelem [1] v polovině 20. století. V závislosti na plynulosti zaoblení se výtokový součinitel μ dle publikovaných výsledků pohybuje v rozmezí 0,75 až 0,95. Kromě samotné kapacity výpustného objektu má však tvar přechodového prvku zásadní vliv na výšku provzdušněného válce vody v patě šachty a tím i na tlakové pulzace v samotném přechodovém prvku.

Tvary přepadových paprsků pro plně zavzdušněný přepad přes ostrohranný kruhový přeliv publikoval Wagner také v polovině 20. století [2] a umožnil návrh tvaru beztlakových přelivných ploch pro šachtové přelivy. Řada projektantů nevyužila Wagnerových výsledků, což vedlo k realizaci přelivů, na nichž v určitém rozsahu hladin vznikají na přelivné ploše podtlaky [3, 4]. Tvar přelivné plochy, včetně možných usměrňovacích prvků, ovlivňuje charakter proudění v samotné šachtě, okamžik zahlcení, respektive přechodovou oblast a vznik spirálního proudění.

Rozvoj numerických metod spolu s klesajícími výpočetními náklady umožnily získání konsumpčních křivek šachtových přelivů na základě numerických simulací [5]. Výsledky získané pomocí dvoufázové CFD simulace s k-w SST modelem turbulence a nehomogenním rychlostním polem prokázaly dostatečnou přesnost a jsou často využívány, např. [6]. Určení tlakových pulzací a možného periodického namáhání konstrukcí pomocí CFD je však možné pouze za předpokladu respektování všech relevantních okrajových podmínek, tj. morfologie nádrže, geometrie objektu přelivu a při využití neustáleného výpočtu [7], který je ovšem stále časově náročný.

2. Spirální a axiální proudění a tlaky

Pro výpustná zařízení procházející tělesem sypaných hrází představují tlakové pulzace a možné vibrace namáhání, které je vhodné maximálně omezit. Zejména pro přehrady se zemním těsněním je riziko rozvoje vnitřní eroze podél vibracemi namáhaného prvku nepřijatelné. Průměrné hodnoty tlaků uvnitř šachty nebo přechodových prvků jsou obecně méně podstatné, jsou-li pozitivní, než hodnoty pulzací.

Vyloučíme-li vliv morfologie nádrže a potenciálních usměrňovacích prvků a budeme tedy předpokládat dokonale symetrické nátokové poměry, pak proudění uvnitř šachty bude mít charakter axiální při volném nezahlceném a přechodovém režimu. Při zvyšující se hladině a zatápění vtoku dochází ke vzniku nestabilního víru.

Tlakové pulzace působící na stěny šachty v případě stabilního spirálního proudění jsou dle výsledků jiných autorů, např. [8] či [9], podstatně nižší než v případě proudění axiálního. Naproti tomu spirální proudění ve srovnání s axiálním omezuje kapacitu v důsledku redukce části profilu pod vírem. V případech, kdy výpustné zařízení neprochází tělesem hráze, a ani z jiných důvodů nejsou tlakové pulzace podstatné, jsou často navrhovány konstrukce bránící tvorbě víru v průběhu zahlcování, čímž je zvýšena kapacita výpustného zařízení.

Rigorózní analýza vlivu tvaru a počtu usměrňovacích a přechodových prvků na tlakové pulzace je náročná a absence obecně platných doporučení vede při návrhu obvykle pouze k ověření, že navržený tvar poskytuje přijatelné výsledky v průběhu povodňových událostí. Obtížně postihnutelný parametr při tvorbě obecných doporučení je zejména tvar nádrže. Takovýto postup poskytuje sice vhodné výsledky při samotném návrhu vodního díla, ale přináší značné obtíže při posuzování stávajících konstrukcí a následné rizikové analýze. Starší vodní díla obvykle nesplňují moderní požadavky na bezpečnost za povodní a stavební úpravy, které nelze podložit bez dalšího modelování, jsou často nezbytné pro zajištění splnění aktuálních požadavků.

3. Režimy proudění a jejich hranice

U šachtových přelivů rozeznáváme tři základní oblasti režimů proudění. Oblast nezahlcená, respektive nezatopeného přepadu byla vymezená Wagnerem [2] nerovností , kde h (m) představuje výšku hladiny nad korunou přelivu a D (m) je průměr půdorysu koruny přelivu. V této oblasti je vztah mezi průtokem a výškou hladiny řízen standardní rovnicí přepadu se součinitelem přepadu m (-) a gravitačním zrychlením g (m.s-2).

Zatopený přepad je vymezen nerovností a vztah průtoku a hladiny lze popsat rovnicí výtoku otvorem, tj. resp. , kde Ds (m) je průměr svislé šachty, H (m) je tlaková výška nad kritickým profilem před zavzdušněním (pokud je tlakové proudění zajištěno i v odpadní chodbě, pak nad výtokem z chodby), μ (-) je výtokový součinitel a Sz (m2) je plocha kritického profilu (je-li menší než profil šachty).

Přechodová oblast mezi zcela neovlivněným a kompletně zatopeným přepadem, který přešel do výtoku otvorem, se vyznačuje následujícími charakteristikami:
• pro v čase konstantní průtok dochází k významné změně v poloze hladiny, tj. rozsah hladin lze pozorovat při konstantním průtoku;
• vztah mezi průtokem a hladinou vykazuje hysterezní chování v závislosti na tom, zda se systém zahlcuje, nebo uvolňuje.

Obě výše uvedené nerovnosti pro neovlivněný a zatopený přepad lze najít v řadě inženýrských publikací, např. [10]. Je ovšem třeba uvážit, že obě hranice byly odvozeny na modelu s ostrou přelivnou hranou, a přestože spodek paprsku byl dostatečně zavzdušněn, obecnou platnost těchto nerovností pro určení režimů proudění na reálných konstrukcích lze zpochybnit. Případová studie prezentovaná v následující kapitole nejen vykazuje odlišných hranic pro režimy proudění, ale dokazuje možné ovlivnění těchto hranic dalšími konstrukčními součástmi výpustného komplexu, tvaru přechodových prvků a režimu proudění v odpadní chodbě.

4. Fyzikální model šachtového přelivu VD Jirkov

VD Jirkov bylo zhotoveno mezi lety 1960–1965 a tvoří je 55,6 m vysoká sypaná kamenitá hráz s ukloněným středním zemním těsněním a výpustná a odběrná zařízení sdružená do věžového objektu. Šachtový přeliv věžového typu s kruhovým půdorysem přelivu o průměru 9,4 m a proudnicovou přelivnou plochou přechází u dna kolmým napojením na odpadní chodbu ve sklonu 2 %, které předchází zúžení profilu a odtrhová zavzdušněná hrana. Spodní výpusti jsou vyústěny z obou stran do odpadní chodby v místě zúženého profilu těsně před odtrhovou hranou.

Komplex výpustných zařízení obsahuje řadu atypických prvků. Například dlouhé, ale nízké 4 usměrňující konstrukce sahající až do hloubky 9,0 m, jejichž účelem je zřejmě zajistit spirální proudění. Samotnou přelivnou plochu lze pro velkou škálu průtoků považovat za podtlakovou (přibližně pro přepadové paprsky tl. 0,5–1,1 m). Prvotní úlohou hydrotechnického výzkumu na fyzikálním modelu 1 : 20 při zachování Froudova zákona modelové podobnosti bylo ověření hydraulických podmínek při stávajícím stavu konstrukcí. Výsledky výzkumu prokázaly výraznou diskrepanci mezi konsumpční křivkou systému předpokládanou v rámci dokumentace díla, jež se opírala o konstantní součinitel přepadu, a křivkou stanovenou na základě měření na modelu. V průběhu měření se dále prokázala nevyhovující funkce stávajících usměrňující prvků, které nebyly schopny vytvořit stabilní spirální proudění ani pro nízké, ani pro vysoké průtoky. V průběhu zahlcování byl pozorován vznik víru s opačnou rotací, než odpovídá tvaru stávajících usměrňovačů. Vybrané výsledky první části hydrotechnického výzkumu byly publikovány v rámci mezinárodní přehradní komise ICOLD v roce 2016 [11].

Doplňující část výzkumu, jejíž vybrané výsledky jsou prezentovány níže v tomto článku, detailně studovala vliv konstrukčních úprav na vtokové a přechodové části na tvar konsumpční křivky a tlakové pulzace spojené s rizikem vibrací.

4.1 Úpravy modelu a zkoumané varianty

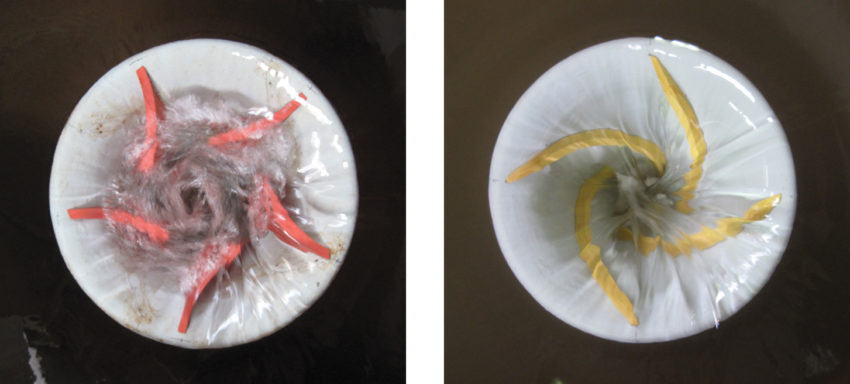
Vtoková část modelu, jejíž stávající tvar je včetně usměrňujících žeber patrný z obrázku 1b, byla upravena odebráním usměrňujících elementů a posléze jejich náhradou upravenými 5 nebo 6 novými prvky, viz obr. 2. Nové systémy usměrňovacích prvků byly testovány v krajních variantách pootočení vůči ose odpadní chodby. Obrázek 2a znázorňuje systém uchycení umožňující pootočení a následnou fixaci pro další experimenty.

Obr. 1. BP VD Jirkov, (a) vtoková část – skutečnost, (b) vtoková část s usměrňovací prvky – model

Obr. 2. Model vtokové části BP VD Jirkov, (a) šest usměrňovacích prvků s možností změny polohy vůči ose odpadní chodby, (b) varianta s 5 usměrňovacími prvky

Kromě měření základních veličin, tj. průtoku (indukčním průtokoměrem a kalibrovanou dýzou) a hladiny vody v nádrži, byly sledovány hladiny uvnitř odpadní chodby a v navazujícím korytě. Uvnitř šachty a podél odpadní chodby byly dále měřeny tlakové pulzace pomocí 16 sond s frekvencí snímání od 1 do 1000 Hz. Polohu sond znázorňuje obrázek 3.

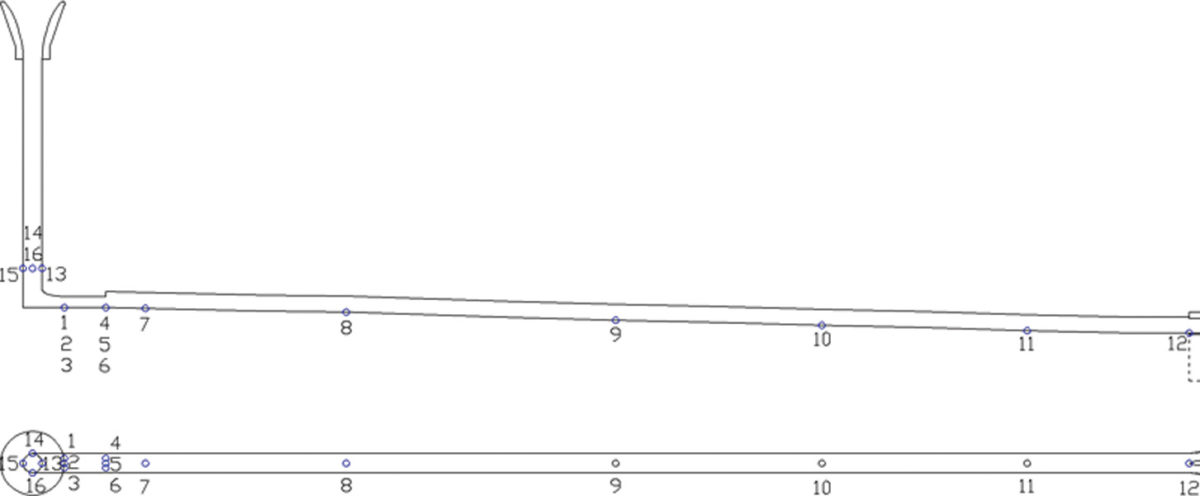
Obr. 3. Schéma rozmístění tlakových sond na modelu

V rámci modelu byl dále sledován vliv úpravy přechodového prvku z ostrého zalomení, které představuje stávající stav, na maximálně konstrukčně proveditelné hydraulicky vhodné zaoblení reprezentované poměrem R/Dš = 1,13. Celkem bylo provedeno měření na 32 různých variantách uspořádání modelu pro celkovou škálu povodňových průtoků až po zatopení a zahlcení přelivu.

4.2 Konsumpční křivky a hranice zahlcení – vybrané výsledky

Vliv jednotlivých testovaných uspořádání na konsumpční křivku přelivu je zřejmý z grafu na obr. 4. Zatímco úprava přechodového prvku na hydraulicky příznivější má pozitivní dopad na kapacitu a oddálení zahlcení systému, usměrňující prvky omezují kapacitu o 4–5 % v oblasti s neovlivněným přepadem. Nově zkoumaná úprava s 5 usměrňovacími prvky ovšem zároveň výrazně oddaluje samotný přechod do zahlcení. Měřené hranice jednotlivých režimů proudění shrnuje následující tabulka 1.

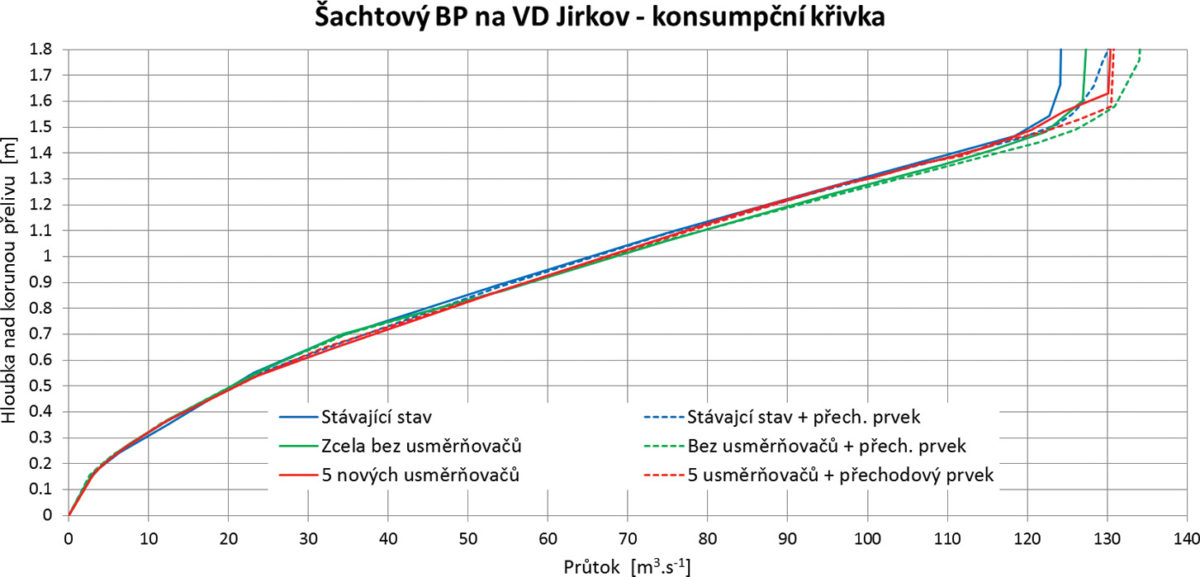
Obr. 4. Konsumpční křivky pro vybrané varianty modelu

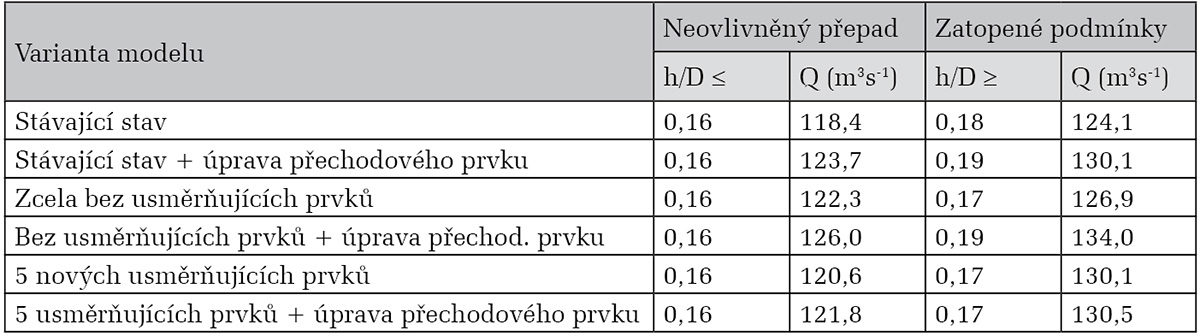
Tab. 1. Hranice režimů proudění – výsledky modelu

Z výše prezentovaných výsledků je zřejmé, že význam hydraulicky vhodného tvaru přechodového prvku je vyšší u axiálního proudění a nižší u proudění spirálního. Z tabulky 1 rovněž vyplývá, že využití obvyklých nerovností ohraničujících režimy proudění by v tomto případě bylo zatíženo významnou chybou.

4.3 Tlakové pulzace

Vyhodnocení významu tlakových pulzací lze provést ze dvou odlišných úhlů pohledu. Jednak pomocí čáry překročení pulzací v závislosti na průtoku, která nám umožnuje stanovit pravděpodobné namáhání konstrukcí. Je nezbytné zdůraznit, že tyto čáry překročení se liší pro konstantní průtok v jednotlivých sondách a případné srovnání variant musí vzít v potaz nejen průtok, ale i polohu sondy.

Obrázek 5 prezentuje příklad výsledků pro 6 různých testovaných variant při shodném průtoku odpovídajícímu ve skutečnosti Q100 (tj. 33,1 m3.s-1). Pro tento průtok je poměr h/D roven 0,095 a průtok tedy bezpečně spadá pod neovlivněný přepad. Z grafu je patrný vliv zaoblení přechodového prvku na tlakové pulzace v šachtě.

Graf na obrázku 6 znázorňuje velikost a pravděpodobnost překročení tlakových pulzací při průtocích Q20 a Q1000 (13 a 74 m3.s-1). Z grafu je patrné, že stabilní spirální proudění, ke kterému dochází při instalaci 5 usměrňovacích prvků spolu s hydraulicky vhodně zaobleným přechodovým prvkem, se vyznačuje nižšími tlakovými pulzacemi. Zároveň je z obr. 6 patrné, že pulzace jsou do průtoku Q100 velmi malé.

Obr. 5. Čáry překročení tlakových pulzací v sondě 15 při průtoku Q100

Obr. 6. Čáry překročení tlakových pulzací v sondě 15 při průtoku Q20 a Q1000

Druhým pohledem pro zkoumání tlakových pulzací je riziko vzniku oscilací způsobených pulzacemi s dominantní frekvencí. Oscilační namáhání má potenciál k poničení stavby, zejména v oblasti dilatačních spár, a zvyšuje riziko vzniku vnitřní eroze podél objektu procházejícího hrází.

Obrázek 7 prezentuje problematický vznik oscilačního namáhání s dominantní frekvencí přibližně 0,5 Hz. Tento fenomén je ovšem silně závislý na průtoku a při ostatních testovaných průtocích nebyl pozorován. Průtok Q10000T při této variantně uspořádání má poměr h/D rovný 0,136 a může tedy být považován za dokonalý přepad. Srovnání hladin při různých variantách a průtoku Q10000T zobrazuje obrázek 8.

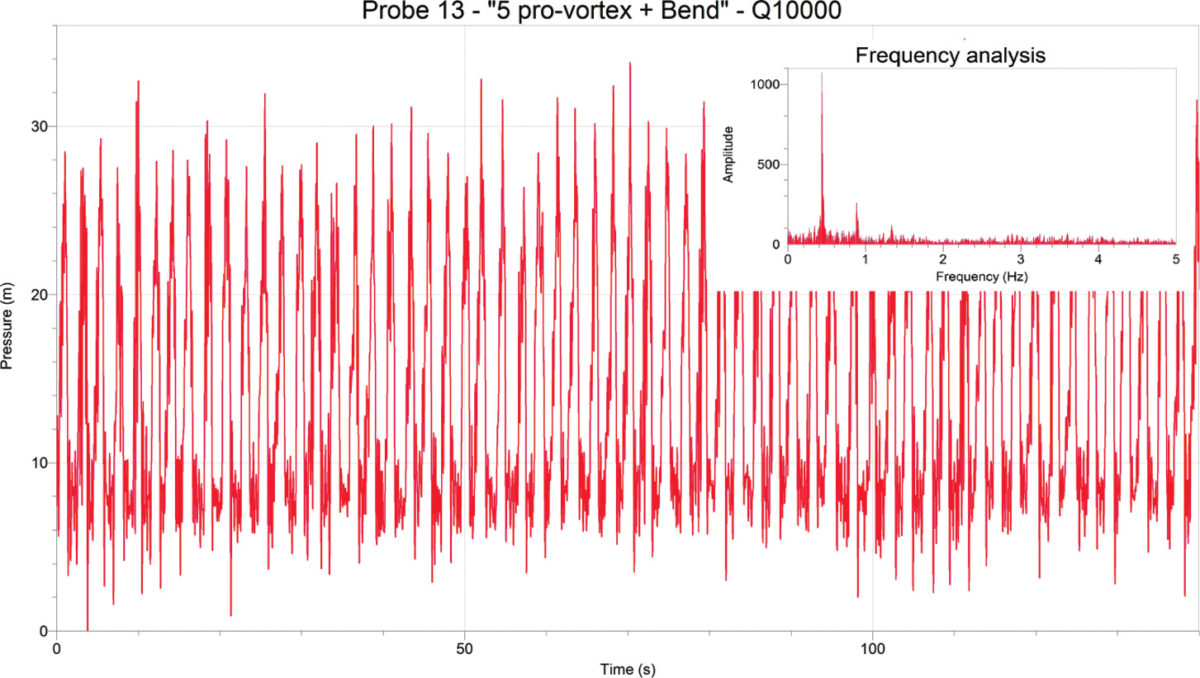
Obr. 7. Měřené hodnoty tlaků a FFT analýza pro průtok Q10000T a nové usměrňovací prvky

Obr. 8. Vtok BP VD Jirkov při Q = 95 m3.s-1, tj. Q10000T, (a) pět usměrňovacích prvků, (b) stávající stav

Tlakové pulzace mohou být dále spojovány s uzavřeným strženým vzduchem, který postupuje vzhůru šachtou a umožňuje vznik gejzírů (blowbacks). Z pozorování na modelu lze učinit závěr, že ke vzniku gejzírů dochází častěji než ke vzniku oscilací.

5. Závěr

Hydraulické podmínky v komplexních výpustných zařízeních s usměrňovacími prvky nelze popsat obecnými rovnicemi s dostatečnou přesností. Korektní odhad nevyžaduje jen součinitel přepadu závislý na tvaru přelivné plochy a poměru h/D, ale i vliv hydrodynamických tlaků a možných pulzací, které bohužel nejsou symetricky uspořádány podél šachty.

Výsledky fyzikálního modelu prezentované v článku potvrzují, že tlakové pulzace v šachtě a na dně odpadní chodby jsou při spirálním proudění nižší než u proudění axiálního. Počet, tvar a pozice usměrňovacích elementů jsou podstatné, ovšem optimální uspořádání závisí i na tvaru nádrže. Dále byl prokázán vliv zaoblení přechodového prvku. Pro většinu sond a průtoků je tento vliv pozitivní.
Potíže se strháváním vzduchu a opačným prouděním vzduchu (slug flow) v šachtě byly signifikantně větší při instalaci usměrňovacích prvků.

Poděkování: Příspěvek byl zpracován v návaznosti na výzkumný projekt financovaný Ministerstvem vnitra ČR č. VG20102014056 a autoři příspěvku tímto vyjadřují svou vděčnosti poskytovateli. Autoři by rádi poděkovali Povodí Ohře, státnímu podniku, v jehož správě je VD Jirkov.

Literatura/References
[1] Gardel, A, (1949). Les évacuateurs de crues en déversoirs circulaires, Bulletin Technique de la Suisse Romande, (27).
[2] Wagner, W. E., (1954). Morning-Glory Shaft-Spillways. Determination of Pressure – Controled Profiles, Proceedings ASCE, vol. 80 (432).
[3] Tanchev, L. (2014). Dams and Appurtenant Hydraulic Structures 2nd Ed., CRC Press, Leiden, NL.
[4] Satrapa, L.; Brouček, M.; Králík, M.; Kučerová, J.; Zukal, M.; Horský, M. (2015) VD Jirkov úprava dopadiště šachtového přelivu – modelový výzkum, Závěrečná zpráva, 11/2015.
[5] Ackers, J., Bennett, F. and Khan, J. (2013) Hydraulic design issues in raising the morning glory spillway of Chaffey Dam. IPENZ Proceedings of Technical Groups 39. Multiple Use of Dams and Reservoirs: Needs, Benefits and Risks.
[6] Rafiee, S.E.; Sadeghiazad, M.M. (2014) 3D cfd energy analysis of the performance of a counter flow vortex tube, Int. J. Heat and Technology, 32(1–2), pp 71–77.
[7] Skarupova, E., Nowak, P. (2016) Physical and mathematical modelling for aided overspill redesign, Hydro 2016 – Achievements, opportunities and challenges. Hydro 2016. Montreux, Aqua-Media International Ltd. 2016.
[8] Haindl, K & Dolezal, L (1961). Turbulent pressure fluctuation in a complex hydraulic structure. Proceedings of the 9th IAHR General Meeting, Dubrovnik, pp 56–65.
[9] Novak, P., Cabelka, J. (1981) Models in hydraulic engineering physical principles and design applications London, UK: Pitman Publication.
[10] Novak, P., Moffat, A.I.B., Nalluri, C. and Narayanan, R. (2007) Hydraulic Structures 4th ed.; Taylor & Francis.
[11] Broucek, M., Satrapa, L., Zukal, M., Kralik, M. (2016) Existing Shaft Spillway Enhancement Based on Physical Modelling, Proceedings of the International Symposium on “Appropriate technology to ensure proper Development, Operation and Maintenance of Dams in Developing Countries”. Pretoria: SANCOLD, pp. 311–320.

Ing. Miroslav Brouček, Ph.D.
(autor pro korespondenci)
Ing. Martin Králík, Ph.D.
doc. Ing. Ladislav Satrapa, CSc.
Katedra hydrotechniky
Fakulta stavební
ČVUT v Praze
miroslav.broucek()fsv.cvut.cz